Chapter seven
What does a memory
look like?
Fourier transform of a literal image of a duck, courtesy of Kevin Cowtan. The Fourier Duck originally appeared in a book of optical transforms (Taylor, C. A. & Lipson, H., Optical Transforms, Bell, London 1964). An optical transform is a Fourier transform performed using a simple optical apparatus. In the memory hypothesis to be presented here, the “simple optical apparatus” is the lens of the human eye.
Images from waves
It is surprising that so few of us are ever exposed to a wave-optical version of how images form. Even students of physics don’t get much of a glimpse, in basic texts, of the physical basis of image formation. Optics presented in general biology texts is largely based on ray tracing. Diffraction is mentioned in a sidebar, essentially as a nuisance effect which puts a limit on resolution. There is rarely a hint that the whole process of imaging is based on diffraction.
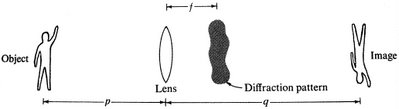
Here is the main element that is missing from the ray-tracing approach and story. Notice in the following illustration the blob marked “diffraction pattern” hovering behind the lens (figure adapted from Elementary Wave Optics, by Robert H. Webb, Dover, 1997).
How and why should a diffraction pattern appear in the focal plane (at the distance f) behind the lens? What produced it? What is it good for?
It turns out the diffraction pattern is the product of an extra optical device which has been inserted into the system as a theoretical convenience: This system is acting as though a diffraction grating had been mounted in front of the lens, although in fact no grating is literally present.
It is quite a story. In the early 1870s, Ernst Abbe, the genius behind Zeiss, noticed that certain specimens studied under the microscope were highly periodic in structure. An insect scale is a good example.
Colorized SEM of a butterfly’s wing scale. Photo courtesy of Tina Weatherby Carvalho, Biological Electron Microscope Facility, U. Hawaii
It occurred to Abbe that an insect scale could be understood as, or simply declared to be — not just a tissue specimen but an optical device: a diffraction grating. By thinking about an insect scale in this novel and very special way, and by assuming coherent light conditions, Abbe realized he could freely apply to the mystery of image formation the known mathematics of diffraction gratings.
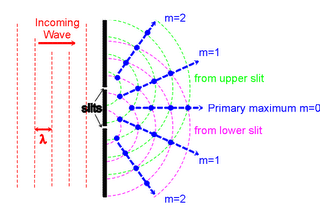
The straightforward geometric math worked out by Thomas Young in the early 19th century to describe the results of his two-slit experiment works equally well in describing the interference effects of light passed through multiple slits – diffraction gratings. Abbe applied Young’s formulation. What emerged was a description of image formation as an effect produced by light wave interference.
It is now called the double diffraction theory of image formation. Light wave interference occurs in two places: The first interference occurs behind the lens in the diffraction plane (the “blob” remarked in the figure). The second interference occurs at the image plane, and produces bright points of light — Airy circles. An image plane populated with these bright points of light produces an image.
So our understanding of image formation is based on a rather startling assumption – that all sorts of objects on display might be successfully modeled as diffraction gratings intervening between a coherent light source and a converging lens.
This assumption was useful because it put into the hands of Ernst Abbe a huge mathematical short cut provided by Young’s handiwork on diffraction at slits. The Abbe assumption is clearly based on a very special case. Most objects are not, after all, insect scales or other types of diffraction gratings, and most light is not coherent for long. We do not view the world through a venetian blind. But Ernst Abbe was on the right track.
Any sort of object can be said to diffract light — diffraction is universal, not unique to diffraction gratings.
Although the light of the world is not coherent, it is partially coherent, and one can describe the system in terms of instantaneous fringes with continuously changing positions. Nice sharp interference bands are best demonstrated by beaming, at parallel slits, coherent monochromatic light from a laser. In our messy, partially coherent, polychrome world the bright and dark bands do appear, but their appearance at a given point is merely instantaneous. For this reason the bands are imperceptible to us. But they exist.
Abbe’s treatment of image formation has stayed glued for over 142 years.
In a paper published in 1906, A.B. Porter built upon Abbe’s idea. Porter proposed that Abbe’s two planes, the diffraction plane and the image plane, could be interpreted using the Fourier series: It turns out that the image on the image plane is the Fourier transform of the diffraction pattern on the diffraction plane. The diffraction plane is now often called the “Fourier plane.” It is also called the “back focal plane” of the lens.
The double diffraction theory was refined and given its name by the Dutchman Frits Zernike in 1935. Zernike ultimately won the Nobel for inventing phase contrast microscopy, but his earlier work on double diffraction image formation seems more fundamental.
In the end Abbe’s theory was successfully generalized to include non-periodic objects and partially coherent light – the objects and lighting of the real world.
The theory is still introduced by showing how an image is formed by a very special and specific type of object, a diffraction grating, illuminated by coherent light. Here is what Abbe came up with – an iconic picture you will find again and again in explanations of image formation.
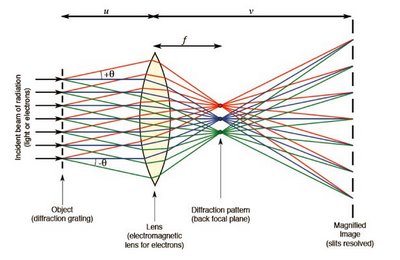
Thanks to the diffraction grating, or “object,” light waves interfere at the back focal plane of the lens. Wave interference produces bright and dark interference bands there. The bright bands act as point sources of light. Rays drawn from point sources in the back focal plane of the lens will converge with rays drawn from other point sources that arise simultaneously at the back focal plane.
These rays converge at points on the retina. At these points a second wave interference occurs, resulting in bright points of light imprinted at the retina. It is the picture dotted-in by these secondary bright points on the retina, the Airy circles, which we perceive as an image.
as slang physics
In fact there are always two planes behind the lens, the image plane and the back focal plane, and the image always forms on the image plane. An image never forms on the focal plane
When students get a first look at the wave optical model of image formation, they often wonder why a diffraction pattern should suddenly appear on the focal plane of the lens. They have been taught an image is supposed to appear on the focal plane. But this is just physics slang.
Practical logic supports the slang treatment of “the focal plane” as though it were the image plane, and this is probably why the misconception is so common. To see the reasoning, start with this animation of a converging lens system. If you push the slider to the left, you can see the object recede toward the western horizon. As it does so the image plane advances toward the back focal plane of the lens. Conversely, as the object is brought nearer to the lens, the image plane retreats further behind the focal point, so that the focal plane and image plane become well separated. (The planes are represented here as points, which lie on the respective planes.)
As an object recedes into the distance, according to the thin lens equation, the image plane and the focal plane get closer and closer together until finally, when the object is “essentially at infinity,” the two planes can be regarded for all practical purposes as one single plane called, very unfortunately, “the focal plane.”
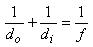
In detail, d sub o is the distance to the object; d sub i is the distance to the image; and f is the back focal length. As d sub o approaches infinity, the denominator explodes and the term becomes, practically speaking, zero. Negligible.
This makes the distance to the image plane identical to the distance to the focal plane. So now you can get away with saying the image forms on the focal plane. This is the formal logic behind the lazy vernacular of photographers and physics teachers and, to be candid, almost everyone else including me, that would put the image on “the focal plane.”
But it never happens. An image never forms on focal plane, and the two distinct planes always exist. As long as an object is this side of infinity (and they always are), its image will always form on the image plane, and both the focal plane and the image plane will always exist.
Note too from the animation that as the object heads toward infinity, the image on the image plane shrinks. An infinitely distant object would produce an infinitessimal image, yes? This is just another way to say the same thing, which is that an image never appears on the focal plane.
In wave optics, it matters. This is because you need both planes, the back focal plane and the image plane, to make the wave-optical machinery of imaging work.
To add further confusion, the “back focal plane” has two more names, “diffraction plane” and “Fourier plane.” You just have to be alert to all this terminology.
Finally, bear in mind that the focal plane is not flat. It is curved in 3-space like the backwall of the eye, and this is essential. To create an image that is actually flattened, as it must be on camera film, requires serious optical design work.
Optics is so full of tricks and traps that physics educators have done studies in an effort to try to figure out why this particular body of knowledge is so difficult to convey from teacher to student. One reason is that the nomenclature of optics is not precise.
The distance between the two planes
It is clear from the double diffraction diagram that the back focal plane and the image plane are well separated in Abbe’s Zeiss microscope. The thin lens equation tells us to expect a substantial separation between the two planes when very near objects are imaged. In fact in a microscope there is sufficient space between the two planes that it is possible to insert additional hardware to get a look at the diffraction pattern at the back focal plane. This can be accomplished by positioning a half-silvered mirror at the microscope’s back focal plane.
For the human eyeball, unlike a microscope, the object to be imaged is relatively distant. For this reason the focal plane and the image plane are very close together. The close proximity of the two planes is maintained, in the optical system of the eye, by accommodation.
Here the rays are shown converging to a single point on the image plane. Lots of points like this one would constitute an image. The back focal plane is not even shown — it has been merged, as usual, and for everyone’s convenience, into “the focal plane.”
We know the real back focal plane must lie somewhere between the image plane and the lens, but where exactly? How close are the two planes?
This picture is accurate in the sense that the two planes (points) are so very close together they cannot be separately drawn by an artist with a thick pencil. Both critical planes, that is, back focal plane and the image plane, stack up on the retina.
Two planes, two pictures and
the point of it all.
The retina is about as thick as of a sheet of paper, which is pretty thick at the working scale of a light wave. The outer segment of a human retinal rod is nominally about 25 microns long, so we can take this as the thickness of the photosensitive layer of the retina. Within the z-axis boundaries of the retina, we have positioned two planes, the diffraction plane and the image plane.
Let’s guess the retina senses the play of light on both of these two distinct planes, separately and simultaneously.
The literal picture on the image plane is what we see. The interference pattern on the back focal plane (i.e., the diffraction plane) is what we store.
How to model a Fourier Transformer?
On the planet where I live, each neuron has 300 or more numbered channels.
The brain receives, instantly recognizes and transmits analog levels we can readily represent as numbers. It is an immensely fast and competent analog computer. It reads the senses, calculates, and issues exact motor commands, all with enormous speed and facility.
The retina detects spatial phase. And each cerebral hemisphere is a glorified, stratified stack of quasi-retinas.
This is a very different hypothetical machine from the nervous system as it was understood in 1963 or as it is accepted today.
This brain is analog-incremental. It has the calculating speed of an analog computer and the clean data transmission of a digital computer. Each single spike represents a number, an integer, and the number does not have to be 1 or 0. It could be 247.
The first place to look for an interference pattern in the human brain is in the eye, in the diffraction plane (back focal plane) of the lens.
It is this interference pattern that is ultimately recorded in the brain, in distributed fashion — as distributed memory. This type of memory is content addressable. The subtle curve of your beloved’s cheek is sufficient, as input, to retrieve from memory the 3-dimensional whole of your beloved.
The culminating step of remembering consists of Fourier transforming the interference pattern back into a sharp literal, spatial image.
The whole process depends on phase conservation, but we have provided for this, on our planet, by wiring every single light sensitive disk in each photoreceptor of the retina. The retina is not just a light sensitive 2-dimensional plate, like photographic film. It has a z-axis. It is a sensitive solid.
What is a memory?
If you can agree with a brilliant hunch, then I agree fundamentally with the basic intuition of Karl Lashley and the holographic memory theorists: Memory is a stored interference pattern corresponding to a literal image.
But it is not an interference pattern made by mixing a scattered wave with a pure, coherent reference wave, as in benchtop Holography. Nor is it produced in the nervous system by electrical wave interference on the dendrites.
It is simply a light interference pattern produced in an Abbe imaging system at the Fourier plane, or back focal plane, of the lens in the eye.
So on my planet, this is a memory: The interference pattern corresponding to a literal image (of a duck in this case) is the thing to be remembered.
The memory could retain both of these two pictures readily enough, and it might well do so in the short term or even indefinitely. But it is the interference pattern which can constitute a durable long term memory resistant to injury and insult. This is because the interference pattern encodes the duck in distributed fashion.
Recall from Chapter 6 the metaphor of the smashed lens. Any small, surviving fraction of this interference pattern can be Fourier transformed into the whole, familiar spatial image of a remembered duck. The interference pattern is also susceptible to filtering and processing steps for feature extraction, edge detection, and image cleanup. Finally it could be the basis of a content addressable retrieval system in the manner of Van Heerden’s.
In this hypothesis, both the interference pattern and the literal image fall within the thin depth of the retina, on the focal plane and the image plane of the lens, respectively — one plane stacked close behind the other.
The focal plane of the retina is the memory’s doorstep and precisely here, on this doorstep, nature has delivered an interference pattern, ready to store and process.
What is new here?
The idea that the brain processes and remembers interference patterns has been kicking around, in and out of vogue, for the past 82 years and you can find in the literature quite a range and variety of brain hypotheses rooted in Karl Lashley’s basic intuition of 1942. Fourier transformation seems to figure into all of these streams of ideas at some point.
In the visual system, the usual assumption is that the eye captures a literal image and the brain, subsequently, transforms it by calculation into the frequency domain. The retina is conceived conventionally, and is capable of detecting only one plane — the image plane.
The Fourier plane in the eye is invariably and amazingly ignored in these old models. The brain is supposed to recreate or approximate the interference pattern that is so easily available on the Fourier plane — by running Fourier transform calculations. The calculated interference pattern, once arrived at, is then stored as a memory.
In the present hypothesis, things happen much faster. The interference pattern is not calculated — it is simply detected and stored.
The Fourier transformation is accomplished optically, by the lens of the eye, at the speed of light. The transformation operates on the interference pattern on the Fourier plane, and creates (optically) the literal image on the image plane. You would expect this of any Abbe imaging system.
However, it is proposed that the human retina can detect both the literal image and its Fourier transform simultaneously and in real time. This is new. It implies a bipartite retina.
As noted, its utility depends upon spatial phase conservation and this talent, in turn, depends on a multichannel neuron. In my view it would be impossible to accomplish this work with one-channel neurons.
Note that any subsequent interconversion, in the brain, of a literal image and its Fourier transform doesn’t require much time or technology. This is because both pictures are being captured and, probably, recorded simultaneously and in tandem. The brain could flip back and forth between a literal image and its Fourier transform without any calculation or analog processing at all.
Realtime access to the Fourier plane could be quite useful in the short term (in cueing an associative memory for example), but for Fourier filtering and processing steps (thinking, imagining, remembering) analog calculation would be required of the brain.
Parenthetically, note that the Fourier plane and the image plane are just useful geometric constructs. The two exist at the opposite ends of a continuum — they are not necessarily sensed or stored separately.
So there are several new things here. Lightspeed, a different starting point and order of Fourier transformation, a bipartite retina – and, perhaps mainly, a memory process that is essentially biological in its nature, grounded in eye anatomy, physiology, and evolution.
In lower vertebrates….
Primates and birds and a few other vertebrates, including chameleons, are lucky enough to have evolved a clear-sighted fovea, the special, exceptional and superb apparatus for seeing literal, high resolution images. More is required than a concentration or packing of photoreceptors at the point where the optical axis intercepts the backwall of the eye. There must also be a rearrangement of nerve and vascular tissue to expose the outer segments of the photoreceptors.
About 50 percent of bird species have two foveas per eye and some birds have three foveas per eye, a trick to widen angular range of vision without requiring the animal to move its eye or head. Birds are smart. Crows and parrots are very smart. Interestingly, the exaggerated structures in a bird’s head are its eyes — the cerebral hemispheres don’t add up to much. The brain of a mature African Gray Parrot is the size of a shelled walnut, yet these astonishing animals exhibit many of the cognitive skills we would expect of a 4 or 5 year old human child.
In vertebrates without any fovea — most vertebrates — I would guess the essential signal sought from the retina by the brain is in the frequency domain, on the Fourier plane, although it would be helpful to sample the blurry image plane as well.
These animals must extract a useful image from a murky fuzzy scene owing to the intervening retinal tissue that obscures their photoreceptors and wildly diffuses the incoming light. For these animals, we can guess that the incoming signal from the Fourier plane on the retina would be filtered and transformed, by analog calculation in the brain, into a sharper image of the world. Because the intervening goo is a fixed feature of the animal’s own retina, the filter specification should be constant in every scene, so the delivery of a crisp, useful image could be accomplished very quickly. The whole process could be, in essence, hardwired.
Modern image enhancement software and de-blurring software works on similar principles. One speculates that Fourier de-blurring machinery in vertebrates is truly ancient. It probably evolved before the lens did, when the eye had to function with some other, less wonderful means of manipulating light: e.g. a pinhole, a sieve, a zone plate or a mirror, or some combination of these.
Why are we so intelligent?
At this point it becomes easy to speculate that our intelligence evolved from de-blurring machinery, that is, from Fourier processing hardware in the brain. When the clear sighted fovea finally appeared and made it unnecessary to run the de-blurring machinery all day every day, perhaps this left the Fourier processor of the brain some leisure time to start thinking about things. Mixing and matching, filtering and remembering.
The idea reads like a parody of the walking-upright hypothesis, wherein the evolution of our 2-legged stance freed our hands to make tools, throw things, etc., and the big brain followed.
But anyway, there it is. Maybe we are so smart because we evolved an open fovea, and thus freed for other tasks our already fully-evolved Fourier processors. The fovea provided the innate Fourier processor with the leisure to do things other than de-blurring our vision. This could account for the special intelligence of primates and birds, but one would have to make a more complicated case to explain the intelligence of dolphins. And the question also arises — just how smart is a chameleon? No data. However, I have read that as insect hunters chameleons can be cunning.
The eye evolved long before the ear. However, the cochlear membrane of the ear is understood to be a Fourier analyzer. The cochlear membrane is thus analogous to the Fourier plane of the lens of the eye. Two of our major sensory systems, sight and hearing, prominently feature at their input ends a Fourier analyzer. This is a strong hint from simple anatomy that the human brain is a Fourier machine.
Parsing the retina
There are at least two ways to split the retina into two distinct detectors for the Fourier and image planes, respectively. One would be a detector split into two overlaid tiers, stacked up along the optical axis. This approach would seem to work best for lower vertebrates.
Turtles, for example, have a very thick, multi layered retina. This is understood to be the turtle’s solution to the problem of accomodation without a squeezable lens, but perhaps one could also allocate tiers of the turtle retina to a Fourier plane and an image plane.
For humans, the more logical split of the retina is probably into its center, which is the fovea, and its surround. Essentially, this center-surround split also suggests a functional split between cones and rods.
I have come across one recent hypothesis – other than the one discussed here — in which the retina is able to report to the brain directly from the Fourier plane. It is on the remarkable web site of Gerald Huth.
I think he is on a parallel track, but there are a couple of things that I would have to do differently.
He is detecting the Fourier plane on the fovea. In the human eye, I would prefer to nominate the surround – the rods, essentially — as the detector for the Fourier plane.
In this colorized Fourier transform of the duck, notice the prominent red block of color at the center. In terms of information content, this central red spot is the least interesting part of a Fourier transformed image. It is almost a throwaway. In terms of spatial frequency, that is, detail encoded in the pattern, it is essentially DC– it tells you only the brightness of the image.
The central spot is often called the DC component. It is so strong that film exposed to record a Fourier pattern is often processed into a logarithmic image to reveal the finer, weaker bands that surround the dominant central DC spot.
Suppose we mentally organize a Fourier transformed image by overlaying it with a target pattern.
You can say that the DC component at center of the target is the least informative part of the pattern. As you work outward in rings from the center of the target, you get more and more information encoded about finer and finer details in the original image. The bigger the target, the more interference fringe bands you can accommodate – and the better the detail resolution of a literal image you could recover from the pattern by reverse transforming it.
Where should we put the fovea?
In short, the center of the target, the DC spot, which happens to coincide in the eye with the location of the fovea, is the perfect place to put the fovea. Inserting it there subtracts almost nothing from the information encoded in the interference pattern on the back focal plane. The bigger the target pattern, the better the detail that is retained. The finest, weakest fringes at the outer periphery of the target pattern contain the most finely resolved information to be recovered when the image is recreated.
The machine drawing of the human retina that emerges is a bit like a flashlight seen head-on. At the center the fovea, just 1.5 mm in diameter, is the receptor set for literal images. It senses the image plane. Surrounding it, extending all way out to the edge of the retina, is the much larger (in area) receptor set sensitive to the Fourier plane. Notice the essential 3-dimensional curvature of the Fourier plane, corresponding to the curvature of the retina in the eyeball.
In an idealized version of this system, the two concentric detectors would be offset along the optical axis. That is, the image plane detector would be slightly deeper in the eye, along the z-axis, than the focal plane.
In fact the fovea resides in “the foveal pit.” The pit morphology is produced by peeling back the intervening nerves so that the outer segments of the foveal cones get a clearer view of the incoming light. Whether there is also a tiny additional optically precise offset corresponding to the distance between the focal plane and the image plane, is an interesting anatomical question.
In any event, the human bipartite retina looks very much like the textbook picture of the human retina — with different captions. The fovea is still the fovea, and it is also the image plane detector.
The concentric surround of rods — most of the back of the eyeball — is conventionally allocated for black and white and, especially, night vision. We have newly labeled this part of the retina as the focal plane detector or, more precisely, as the Fourier plane detector. The exquisite sensitivity of the rods is put to work detecting the finest and most subtly varying outer fringes of the interference pattern on the Fourier plane — corresponding to the finest details, or highest spatial frequencies, in the picture being received by the eye.
The memory’s own eye?
In summary, according to the bipartite retina model, the tiny fovea is the sourcepoint of our crisp, conscious view of the world. The foveal surround – all the rest of the retina – is memory’s own sense organ.
Within the foveal surround, from a Fourier plane positioned at a certain depth in the retina, the memory can directly record a densely informational interference pattern. This interference pattern, which constitutes in this hypothesis the substance of human long term visual memory — plays all day on the foveal surround, the unconscious and unsuspected eye of memory.
How plausible is this hypothesis? There is no question a light interference pattern lies in the back focal plane of the lens of the eye. The Fourier plane of the lens exists. Without it, there could be no image. This is just physics. But has a neuroanatomical structure ever evolved that could, in effect, peel the Fourier plane away from the image plane and separately read it out to the brain?
To decipher the interference pattern, the brain must receive both phase and intensity data from the photoreceptor set. A one-channel output neuron cannot handle this job. It would be like trying to play a symphony with a telegraph key. However, we are exploring in this essay the possibilities for a multichannel neuron. The photoreceptor is a specialized neuron. A multi-channel rod cell, ultimately served by a multichannel output line, could indeed detect the Fourier plane effortlessly in real time. It might detect the image plane as well, simultaneously.
In sum, given a one-channel, all or none neuron, nothing works here. The Fourier plane exists — part of the landscape of light in the eye — but it cannot be detected or memorized. On the other hand, given the multichannel neuron assumption, yes, the hypothesis is suddenly plausible and something to conjure with.
I think Karl Lashley was probably right. The visual long-term memory is stored in the brain, in distributed fashion, quite literally in the form of an interference pattern. It is an interference pattern imported into the brain directly from the retina, from the Fourier plane of the lens of the eye.
Glimpses of the Fourier plane?
What drug users report as effects of LSD could be accounted for as a curious, essentially pathological melange of signals from the image plane and the Fourier plane. The hallucinatory shapes and colors famously induced by the drug are pretty much what one might expect to see if the Fourier plane were somehow translated or projected onto, or bleeding into, the image plane. (I should add another possibility — LSD produces a loss or distortion of the spatial phase information we are not supposed to have conserved).Here from Wikipedia is a summary description of effects produced by the drug:“…sensory changes [induced by LSD] include basic “high-level” distortions such as the appearance of moving geometric patterns, new textures on objects, blurred vision, image trailing, shape suggestibility and color variations. Users commonly report that the inanimate world appears to animate in an unexplained way. Higher doses often bring about shifts at a lower cognitive level, causing intense, fundamental shifts in perception such as synesthesia.”
The effect of synesthesia from LSD is interesting in that it suggests the mechanism of memory may indeed be closely involved with the machinery we are exploring here. Flashbacks — unbidden visual images that may recur for weeks or months — suggest a link to visual memory.
Metaphorically, it is almost as though these images did not fit or pack properly in the memory, and kept popping back out of it. The images tend to be symmetrical, characterized as bugs and scorpions and reptiles. The description calls to mind typical themes in aboriginal art, in which paired and symmetrical creatures are nested in and strongly resemble a surround of diffraction patterns.
The best known psychedelic drugs are LSD, mescaline (from peyote) and psilocybin. At this site is an account of the discovery of LSD. It presents juxtaposed molecular structures for these three drugs. The recurring theme is phenethylamine. This is evident for mescaline but the phenethylamine structure can also be discerned in the more complex rings of the ergoline system of LSD. Other psychedelics include the substituted phenethylamines: 2,5-dimethoxy-4-ethylthiophenethylamine; 2,5-dimethoxy-4-(n)-propylthiophenethylamine, and 4-bromo-2,5-dimethoxyphenethylamine.
The uncanny relationship between psychedelic drugs and the perception of diffraction patterns will be developed in a later entry, but there is one optical fact that belongs here, in the discussion of the eye.
The power of mescaline (3,4,5-trimethoxy-phenethylamine) to alter imagery is much diminished for distant objects.
Aldous Huxley, in his long, meticulous essay on his experiments with mescaline, reported that the color and other effects (essentially diffraction pattern effects, one might guess) were induced only when viewing nearby objects.
He rhapsodizes over the intricate details of a flower in a pot.
But a chauffeured evening trip to the top of Mulholland Drive, to view the sunset over Los Angeles under the influence of the drug — was a big disappointment to Huxley. It looked like any other sunset over LA. Beautiful, yes, but not transcendent.
He writes: “…we drove on, and as long as we remained in the hills, with view succeeding distant view, significance was at its everyday level, well below transfiguration point.” But with closer objects, sharp edges and periodicity (a cruise past the repetitive, nearly identical homes in a “hideous” 1950s housing development) the power of the drug re-asserted itself.
It suggests that for near vision, some drug-induced problem with accomodation or adaptation (aperture) — something in Huxley’s eye — was distorting the normal geometrical relationship between the Fourier plane and the image plane. With far vision, the long view, the drug lost its power (we hypothesize) to paint or spill the Fourier plane onto the image plane detector. This seems to be something happening in the eye, rather than in the unlit parts of the brain.
We actually know a little about Aldous Huxley’s eyes. They were damaged by a keratitis in his youth. He was in his late 50s in the early 1950s, when he was working on the Doors of Perception, so his eyes’ ability to accommodate would have been gone. This means that for near objects, one would expect to see some distance open up at the retina between the image plane and the Fourier plane. In the extreme case, for a very near object, the image plane might retreat behind (that is, fall off of) the retinal receptors. If both planes were retreating for some optomechanical reason, the Fourier plane might fall onto the image plane detector, and thus become visible in full-spectrum technicolor.
The thin lens equation is not enough to account for the difference in mescaline’s near/far effects, but maybe it hints at a mechanism, or a way to guess at a mechanism. Withal, a fascinating problem.